WHAT’S LUCK GOT TO DO WITH IT
Exploring the Science of Chance and Skill
By Michael Orkin
Dr. Michael Orkin is a distinguished statistician, author and educator whose career has been dedicated to unraveling the mysteries of chance and probability. With a BA in Mathematics and a PhD in Statistics from UC Berkeley, Dr. Orkin has brought his expertise to academia, industry and public forums alike. A professor emeritus at California State University, East Bay, and currently a faculty member at Berkeley City College, he has published extensively on the mathematics of games and probability, making complex topics accessible to all.
His consulting work in the gaming industry and high-profile invited talks, such as a Google Tech Talk, showcase his ability to translate statistical concepts into practical applications. Whether exploring the intricacies of sports betting, randomness in games or phenomena like synchronicity, Dr. Orkin’s engaging approach brings clarity to the fascinating role luck and skill play in our lives.
In his latest book, The Story of Chance: What’s Luck Got To Do With It?, Dr. Orkin tackles intriguing questions about the nature of luck, randomness and skill. From lottery wins to sports betting and even psychic predictions, his insights challenge how we think about chance in everyday life.
An excerpt from Chapter 13, “Luck vs. Skill,” provides a deep dive into one of the most debated aspects of probability. Is success a matter of talent, preparation or just plain luck? Dr. Orkin offers thought-provoking analysis and practical wisdom to help readers navigate these uncertainties with confidence.
Chapter 13 – Luck vs. Skill
What is Luck?
According to the Oxford Languages dictionary: “Luck is success or failure brought by chance rather than through one’s own actions.” Luck is based entirely on chance. What are “success” and “failure?” One person’s success is another person’s failure. Sometimes we can agree, but not always. The most important part of the definition is that luck, however you define it, is due to chance. If you have success or failure due to skill, or due to cheating, that’s not luck.
We feel lucky or unlucky based on things that happen every day. It doesn’t have to be as spectacular as winning the lottery or getting run over by a bus, but, in a sense, it has to be meaningful. You might think you’re lucky if you wake up and it’s a beautiful day or if you got a raise. You might feel unlucky if you catch a cold or if you lose money at a casino. There are superstitions. Different cultures have lucky numbers (7 in the U.S. and India; 3,5 and 8 in China) and unlucky numbers (13 and 666 in the U.S., 4 in China, 17 in India, 43 in Japan and 39 in Afghanistan). There are superstitious events like stepping on a crack in the sidewalk (unlucky), walking under a ladder (unlucky), meeting up with a long-lost friend (hopefully lucky), and astrological readings that can go either way. Gamblers try to find lucky slot machines and avoid unlucky ones.
Luck is All There Is
Craps is a game of chance, not skill, so if you end up a winner, it’s because you are lucky. We analyzed bets on “7”, that is, that 7 would come up on the next roll of the dice, which has probability equal 1/6 and saw, by the law of averages, that if you keep making this bet, with payoff odds 4 to 1, you will end up losing at the rate of 17 cents per dollar bet. If you’re playing a game of chance like craps, luck is all there is. And, by the law of averages, luck eventually disappears. For the same reason that there are jackpot winners in the Mega Millions lottery, if there are enough craps players, someone will be a lucky winner due to the opportunity presented by many players. But even winners will start losing if they keep playing.
Some gamblers have a more complicated definition of good luck than just winning money. For example, the quote from a Las Vegas gambler, “I hope I break even this week, I need the money,” indicates that a gambler who’s been through tough times might consider himself lucky if he just breaks even. A veteran craps player might feel lucky if she loses, but not as much as the 17 cents per dollar that she’s supposed to lose.
Another gambler might attribute losses to entertainment costs and feel good about the whole thing.
Luck in Everyday Life
I first learned about luck when I was six years old. I had just learned to ride a bike. I was riding down a hill when I suddenly found myself going faster than I could manage. I ended up in the bushes, with numerous scrapes and bruises. When I got home, my mother said, “You’re lucky you didn’t get killed.” My mother had a way of interpreting every non fatal accident as good luck. Was she right? I didn’t feel lucky. Maybe there’s data showing that the average child’s bike crash is worse than mine. In a sense, my mother was right. If I did better than the average kid who crashes their bike, I guess I was lucky, or maybe skilled, which is different from luck. Or maybe only a few young bike riders would crash in this situation, and if they did, their injuries would be less severe than mine. So maybe I was unlucky. Or maybe my mother was thinking about the conditional probability of getting killed given that I got in a nasty accident to begin with.
Suppose you find accident data for young bike riders. Divide the total number of accidents by the total number of bike rides to get “accidents per ride.” This crudely estimates your chance of having an accident if you ride your bike. For example, suppose the average young bike rider has about 1 accident every 25 rides. Suppose you’ve recently gone on 30 rides. Then, based on this data, it wouldn’t be surprising for you to have an accident. Of course, some kids are better bike riders than others and some take more risks than others, so, in addition to luck, skill is a factor. I could have prevented a crash by not riding down the stupid hill in the first place. If I had stayed in bed all day, I would never have had an accident. Or maybe I should have practiced more before riding down the hill.
Sporting events and chess (maybe chess is a sporting event) have both luck and skill. If two professional golfers, two chess players or two football teams of equal ability, compete against each other (or any two contestants equalized by odds or point spreads), luck becomes a factor. The results are difficult to predict. That’s why the contests are exciting, and that’s why people bet on them. Maybe the golf ball took a bad bounce or maybe a pass was deflected and became an interception. Or maybe the referee made a bad call. Even games of skill are subject to uncertainties caused by chance. When you say that you’re lucky to have such a good job or to be with such a great partner, there’s probably more involved than luck. Or maybe you make every decision by tossing a coin. When you say that you’re lucky to have such nice parents, is that caused by chance? You can’t have skill in picking your parents. You don’t have a say in picking them at all. It’s not your fault. It’s the result of genetics and survival of the fittest and whatever other laws of nature are involved, including chance.
Roulette
Like craps, roulette is a game of chance in which no skill is possible. If you play roulette repeatedly, betting, say, on red, in which the probability of winning equals 18/38, and with 1 to 1 payoff odds, you will eventually lose, with your losses averaging 5.3 cents per dollar bet. If you end up a winner, it’s due to luck. Or is it? We discussed Dr. Richard Jarecki [in another chapter of this book -Ed.], who made a fortune betting on roulette wheels for which he had collected data and discovered imperfections. These roulette wheels were biased and didn’t spin randomly. Dr. Jarecki used statistics and took advantage of faulty equipment. He might have considered himself lucky to find the faulty equipment, but, in a sense, his success was due to skill, not luck.
Who’s a better Othello player, my friend or me?
My friend and I used to play the board game, Othello, every week. My friend claimed that he was better than I, and I claimed that I was better than him. How does one decide? First, collect some data. In 100 games, spread out over a few months, I won 67 and my friend won 33. I told my friend that my win record of 67% proved that I’m better. He said that I was just lucky. The way to decide between luck and skill is to compute the pvalue for this result. Assume that I’m lucky until proven otherwise. If that’s the case, then I have a 50% chance of winning a game and so does my friend, and my total wins in 100 games has a binomial distribution (discussed in Chapter 25) [again, another reference to a different chapter in his book -Ed.]. If X = number of wins in 100 games, then the p-value equals:
P(X 67) = 0.0004, or about 1 in 2,500.
This is a significant p-value. In other words, it would be very unlikely to have a record like this just by guessing. So, statistically speaking, my success record was not just due to luck. I was more skilled than my friend.
Sports Betting – What’s Luck Got to do With It?
Games like craps, roulette and lotteries are easy to categorize as games of chance because the player is essentially betting against random numbers: A player in such a game has no strategy that does better on average than random guessing. Blackjack involves both chance and skill. Even though dealing cards from a deck is random, there are strategies based on conditional probabilities arising from cards being dealt that can give a player an advantage. Some app games may involve skill, but how can you tell the difference between a game of chance and a game of skill? How can you tell the difference between luck and skill? If there is no skill, players’ results will be due to chance, with the winners being the ones who got lucky.
I analyzed a game in which contestants wager against the “casino” on the results of sporting events. A player either wins or loses each bet. Let’s say that teams are evenly matched, perhaps due to point spreads, so that an unskilled player has a 50% chance of winning a bet. Whether you’re betting on sports or other events, like the stock market, it’s sometimes not clear whether skill is possible. Although you can show mathematically that there’s no skill in craps and roulette, you can’t use the same argument to decide whether betting on the result of a sporting event is a game of chance or a game of skill. For example, you can research the history of teams and maybe get some insights. You can look at player data and analyze the outcomes of repeated play. Maybe you have knowledge that gives you a better chance of winning than just guessing.
Assume that each contestant has a 50-50 chance of winning a bet and then find a p-value for the results. In other words, assume that the result of each bet is random, like the result of a coin toss, unless proven otherwise. If, under this assumption, some contestants do significantly better than chance allows, you can conclude that this is a skill-based game. (Assume there is no cheating.) With this in mind, call a skilled contestant someone who has a significantly higher win percentage than chance (luck) allows. An unskilled contestant is someone whose win percentage is within the range of luck.
You can always win 50% of the time
Suppose you always toss a coin to pick a team, A or B, to win. Suppose (unknown to you) the probability that A beats B equals 0.75, and so the probability that B beats A equals 0.25. Then the chance you win your bet equals:
0.5*0.75 + 0.5*0.25 = 0.5*(0.75 + 0.25) = 0.5.
You will have the same result for any probability that team A beats team B. So, in repeated coin toss picks, even though you will have winning streaks and losing streaks, you’ll average 50% winning picks, regardless of the strengths and weaknesses of the competing teams.
p – values
Assume that each bet has a 50% chance of winning, as if you were tossing a coin to decide which team to pick. You reject the “luck” hypothesis and conclude that a contestant is skilled if there is an extremely low probability that the contestant could have achieved the observed win percentage just by chance guessing. If this is the case, conclude that something other than chance, namely skill, is present. I found contestants whose performance was better than just being lucky and concluded that this was a skill-based game. This doesn’t mean that chance and luck don’t exist, but rather there are skilled contestants.
Multiple Comparisons
For an analysis like this, you must test many statistical hypotheses, one for each contestant, to determine if that player is skilled. Each player has his or her p-value, determined by the win-loss record for the number of predictions made. If sufficiently low, the p-value indicates statistically that the player is skilled, not just lucky. Since there are multiple statistical tests, sometimes called multiple comparisons, you should do something like adjust the p-value cutoff point that distinguishes skill from luck to account for the opportunity for false positives. As with the tests for psychic powers, if you test enough sports bettors, some will appear skilled just due to chance and the opportunity presented by so many bettors. To avoid this possibility, I made sure that the p-value cutoff between luck and skill accounted for the total number of players. (There are methods for doing this, but we won’t go into it here.)
In the betting data, 32 out of 1,980 contestants had win percentages for the number of predictions they made that were so high as to rule out luck. The other players were either within or below the bounds of chance. These results are consistent with a skill-based game.
“Blackjack involves both chance and skill. Even though dealing cards from a deck is random, there are strategies based on conditional probabilities arising from cards being dealt that can give a player an advantage.”
The contestant with the lowest p-value in Table 1 below had 522 wins in 793 bets, for a 65.8% win percentage. A 65.8% win percentage in 793 predictions just by being lucky has a probability equal to 0 rounded off to 30 decimal places. The 2nd lowest p-value equals 0.00000000000370348197, or about 1 in 270 billion. The 5 lowest p values are in Table 1.
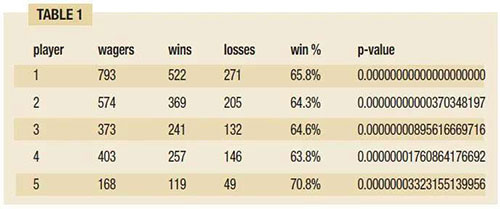
The statistical analysis of the game showed that even when conservatively correcting for false positives, 32 contestants did better than they would just by being lucky. Someone can get lucky and have a higher than 50% win percentage for a while, but in repeated play, luck diminishes. Skill will lead to a long-run win percentage that cannot be attributed to luck. The analysis showed skilled contestants. Luck has its limits. You can show how to detect when someone goes outside these limits.
Bottom Line
Using p-values, you can test whether a gambler is skilled (significant win-loss results in repeated play) or just lucky (results are not significant). However, if you’re testing numerous contestants in a sports betting or other contest, you must account for the opportunity for false positives. If there are some contestants who are skilled at picking winners, as measured by p-values, you can conclude that the contest itself is a game of skill, even if some contestants don’t develop the skills that are available to all.
You can purchase The Story of Chance: What’s Luck Got to Do With It? on Amazon, and Barnes & Noble at www.barnesandnoble.com.
